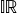
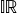
Interval arithmetic consists of a tuple of two numbers representing an infinimum and supremum of an interval. By definition an
interval is in 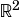 or
or 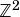 we will however for distinction represent interval numbers as
we will however for distinction represent interval numbers as 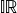 (interval real space) and
(interval real space) and 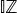 (interval
integer space) as they are used in a distinct manner differing from standard
(interval
integer space) as they are used in a distinct manner differing from standard 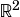 or
or 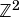 arithmetic. The definition of an interval
is:
arithmetic. The definition of an interval
is:
![- - -
IR = {[x,x]|x,x∈ R,x≤ x}](StabNumRef_PG51x.png)
The two elements in an interval 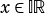 or
or 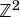 are called infinimum
are called infinimum 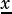 and a supremum
and a supremum 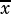 where for a normalized interval
where for a normalized interval
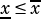 . The two latter are thereby representing the respective infinimum and supremum of an interval hence by definition an
interval
. The two latter are thereby representing the respective infinimum and supremum of an interval hence by definition an
interval 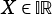 actually defines a set of values:
actually defines a set of values:
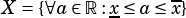
This makes it distinct from 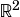 where a number in the latter would correspond to a fixed defined point.
where a number in the latter would correspond to a fixed defined point.