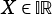 is considered to be bounded if
is considered to be bounded if 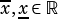 and are finite. If either but not both of
and are finite. If either but not both of 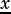 or
or 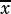 are
are 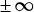 with the
respective sign the interval is considered to be a lower bounded or upper unbounded interval.
with the
respective sign the interval is considered to be a lower bounded or upper unbounded interval.
An interval 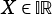 is considered to be bounded if
is considered to be bounded if 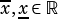 and are finite. If either but not both of
and are finite. If either but not both of 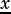 or
or 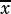 are
are 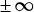 with the
respective sign the interval is considered to be a lower bounded or upper unbounded interval.
with the
respective sign the interval is considered to be a lower bounded or upper unbounded interval.
If 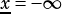 and
and 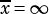 the interval spans the whole
the interval spans the whole 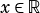 space, this is called a whole interval.
space, this is called a whole interval.
A special case is 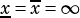 which is by definition an empty interval, as there will be no elements in the resulting interval
set.
which is by definition an empty interval, as there will be no elements in the resulting interval
set.