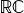
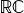
bool disjoint(const rc_interval<T>& a, const rc_interval<T>& b); bool proper_subset(const rc_interval<T>& a, const rc_interval<T>& b); bool subset(const rc_interval<T>& a, const rc_interval<T>& b); bool proper_superset(const rc_interval<T>& a, const rc_interval<T>& b); bool superset(const rc_interval<T>& a, const rc_interval<T>& b); bool overlap(const rc_interval<T>& a, const rc_interval<T>& b); bool inside(const rc_interval<T>& a, const std::complex<T>& v);
These functions assert set properties between two given rectangular intervals 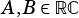 .
.
Whether the two intervals are disjoint to each other.
Determines whether 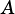 is a proper subset of
is a proper subset of 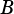 , that is
, that is 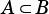 .
.
Determines whether 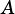 is a subset of
is a subset of 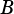 , that is
, that is 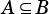 .
.
Determines whether 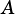 is a proper superset of
is a proper superset of 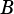 , that is
, that is 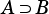 .
.
Determines whether 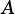 is a superset of
is a superset of 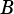 , that is
, that is 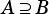 .
.
Determines whether 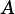 intersects or overlaps with
intersects or overlaps with 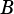 .
.
Whether the complex number 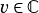 is within the span of the given rectangular complex interval
is within the span of the given rectangular complex interval 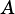 .
.