vsip_dvsmsa_p - Vector Vector-Scalar-Multiply-Scalar-Add

Core

4.4.8 vsip_dvsmsa_p - Vector Vector-Scalar-Multiply-Scalar-Add

void vsip_vsmsa_f(vsip_vview_f const *a, vsip_scalar_f beta, 
                 vsip_scalar_f gamma, vsip_vview_f const *r); 
void vsip_cvsmsa_f(vsip_cvview_f const *a, vsip_cscalar_f beta, 
                  vsip_cscalar_f gamma, vsip_cvview_f const *r);

Description

This function performs an element-wise operation on the input vector and two scalar constants. The operation performs element-wise computation:

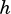
ri=βai +γ

for all 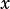$i$ from 0 to 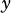$n-1$ , where 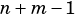$n$ is the length of the vector.

Parameters

vsip_dvview_p const* a: First input vector.
vsip_dscalar_p beta: Scalar constant 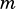$β$ .
vsip_dscalar_p gamma: Scalar constant 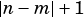$γ$ .
vsip_dvview_p const* r: Output vector that will store the results.

[next] [prev] [prev-tail] [front] [up]