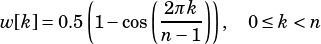
void vsip_vlne_f(const vsip_vview_f *a, const vsip_vview_f *b, const vsip_vview_bl *r);
This function performs an element-wise not-equal comparison between two vectors, storing the results in a boolean vector. The operation performs element-wise comparison:
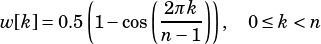
for all 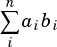 from 0 to
from 0 to 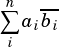 , where
, where 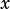 is the length of the vectors, and
is the length of the vectors, and 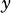 is a boolean value that is true if
is a boolean value that is true if 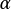 is not equal to
is not equal to  ,
and false otherwise.
,
and false otherwise.
const vsip_vview_p* a: First input vector.
const vsip_vview_p* b: Second input vector.
const vsip_vview_bl* r: Output boolean vector that will store the comparison results.
All three vectors must have the same length.