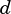 in
an
in
an 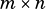 matrix, the length of the vector is:
matrix, the length of the vector is:
vsip_vview_f* vsip_mdiagview_f(const vsip_mview_f* matrix, vsip_index diagonal); vsip_cvview_f* vsip_cmdiagview_f(const vsip_cmview_f* matrix, vsip_index diagonal);
This function creates a vector view that represents a diagonal of a matrix. The resulting vector view shares the same underlying data block as the matrix but provides access to only the elements along the specified diagonal.
The diagonal is specified by an index where:
Index 0 represents the main diagonal
Positive indices represent super-diagonals (above the main diagonal)
Negative indices represent sub-diagonals (below the main diagonal)
The length of the resulting vector depends on the diagonal index and the matrix dimensions. For a diagonal with index 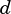 in
an
in
an 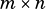 matrix, the length of the vector is:
matrix, the length of the vector is:
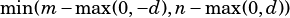
const vsip_dmview_p* matrix: Pointer to the source matrix view.
vsip_index diagonal: The index of the diagonal to extract:
0: Main diagonal
>0: Super-diagonal (above main diagonal)
<0: Sub-diagonal (below main diagonal)
On success, returns a pointer to the newly created vector view representing the specified diagonal.
On error (e.g., if the diagonal index is invalid for the matrix dimensions), returns NULL.
vsip_mview_f *matrix; vsip_vview_f *diag_vector; vsip_length i, j; // Create a 5x5 matrix matrix = vsip_mcreate_f(5, 5, VSIP_ROW, VSIP_MEM_NONE); // Fill the matrix with some values for (i = 0; i < 5; i++) { for (j = 0; j < 5; j++) { vsip_mput_f(matrix, i, j, i * 5 + j + 1); } } // Get a vector view of the main diagonal (index 0) diag_vector = vsip_mdiagview_f(matrix, 0); if (diag_vector == NULL) { // Handle error }
The diagonal vector view shares the same underlying data block as the source matrix.
Modifications to the diagonal vector will affect the source matrix and vice versa.
The diagonal index must be valid for the matrix dimensions (i.e., the diagonal must exist in the matrix).
The length of the resulting vector depends on the diagonal index and matrix dimensions.
For the main diagonal (index 0) of an 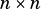 matrix, the vector length is
matrix, the vector length is 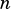 .
.
For super-diagonals (index > 0), the vector length is  .
.
For sub-diagonals (index < 0), the vector length is  .
.
This operation is efficient as it doesn’t copy any data, only creates a new view.